Lesson 07: Latches and Flip-Flops
7.1 Activate Signals
In digital logic design, understanding the differences between level-triggered and edge-triggered signaling is crucial, as these mechanisms dictate how and when a digital circuit, like a flip-flop or a latch, responds to input signals. Here is a detailed explanation of both:
Level-Triggered Signaling
Active High
Active Low
Level-Triggered Signaling
- Definition: A level-triggered device acts or changes state based on the input signal's level (high or low) for the duration it remains at that level. It is useful when continuous monitoring of an input signal is necessary.
- Trigger Level: The predetermined signal level (high or low) at which the output signal activates.
- Active High: A level-triggered device that is active high responds to a high level (logic '1'). It will act or capture data whenever the clock signal is high.
- Active Low: Conversely, an active low device reacts to a low level (logic '0').
- Application:
- Used in simpler or slower systems where timing is less critical.
- Common in latches like the D-latch.
- How It Works:
- The input signal is continuously monitored.
- The output signal is activated when the input signal reaches the trigger level.
- As long as the input signal remains at or above the trigger level, the output signal stays in the triggered condition.
- Advantages:
- Simplicity in design and operation.
- It can be more tolerant of variations in the duration of the input signal.
- Disadvantages:
- More susceptible to noise during the level period.
- This may lead to glitches if the input changes state when the trigger level is active.
- Example: A D-latch is a typical example of a level-triggered device. It captures the input whenever the clock signal (Clk) is high and holds it until it goes low.
Edge-Triggered Signaling
Rising (Positive) Edge Triggered
Falling (Negative) Edge Triggered
Edge-Triggered Signaling
- Definition: An edge-triggered device operates based on the transition or edge of the input signal, either from low to high (positive edge) or high to low (negative edge). It is commonly used in synchronous circuits like flip-flops and counters.
- Trigger Edge: The abrupt change in the input signal (from low to high or high to low) is known as the trigger edge.
- Positive Edge-Triggered: Activates on the rising edge of the clock signal.
- Negative Edge-Triggered: Activates on the falling edge of the clock signal.
- Application: Edge triggering is particularly beneficial when precise timing is required. For example, it ensures that data transitions occur at specific moments.
- Predominantly used in flip-flops like the JK flip-flop, D flip-flop, etc.
- Suitable for more complex and faster digital circuits where precise timing is essential.
- How It Works:
- When the input signal experiences the trigger edge (rising or falling), the circuit responds by switching the output signal to the opposite state.
- The clock signal often picks up this sharp edge to initiate the transition.
- Advantages:
- Immune to noise while the clock signal is high or low, as it only responds to changes.
- It provides better control and stability, reducing the risk of errors in data processing.
- Disadvantages:
- Requires more precise control of signal timings.
- Slightly more complex in design compared to level-triggered devices.
- Example: A D flip-flop is an edge-triggered device. It captures the input at D only at the instance of a clock transition (rising or falling edge, depending on the design) and then holds this value steady until the next triggering edge.
Key Differences:
- Sensitivity: Level-triggered devices respond to the signal level, whereas edge-triggered devices respond to changes in the signal level.
- Timing Requirements: Edge-triggered signaling requires precise timing control to avoid misreads or data corruption, making it ideal for high-speed operations. Level-triggering is less demanding in this respect but more susceptible to noise.
7.2 Latches
Latches, in a Digital Logic Circuits Design course, are fundamental building blocks that serve as temporary storage elements for a single bit of information (0 or 1). They differ from logic gates (AND, OR, NOT, etc.) by their ability to hold a state and are the foundation for more complex sequential circuits. Here's a breakdown of key latch components:
Basic Structure:
Latches typically consist of two or more logic gates (usually NAND or NOR) interconnected in a feedback loop. This loop creates two stable states, allowing the latch to maintain its output (0 or 1) until influenced by external inputs.
Types of Latches:
There are various latch types, each with its own functionalities and control mechanisms:
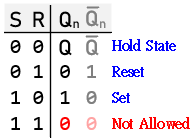
- SR Latch (Set-Reset Latch): Possesses separate Set and Reset inputs for independent control. When both inputs are HIGH (invalid condition), the latch output becomes unpredictable.
- JK Latch: A JK Latch is similar to an SR Latch but has an additional feature that eliminates the indeterminate state in SR Latches.
- D Latch (Data Latch): Offers a Data input and an Enable input. The Enable controls when the latch captures the Data value at its output.
- T Latch (Toggle Latch): Employs a single data input (T) and operates with an enable (EN) signal. On each EN signal (positive or negative depending on design), the T Latch toggles its output (flips between 0 and 1) if the T input is HIGH.
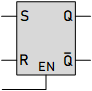
SR Latch
The SR (Set-Reset) latch is a primary type of flip-flop in digital circuits, forming the foundation of memory elements in digital systems. It operates with two inputs, labeled S (Set) and R (Reset), and two outputs, Q and Q. The SR latch can hold a single bit of data to store a 0 or a 1. Here's a detailed explanation of how it works, along with examples:
NOR Type SR Latch
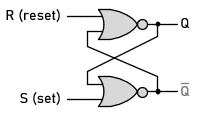
NOR-based SR Latch
- Structure: Comprises two cross-coupled NOR gates.
- Inputs Active High: In this case, the S and R inputs are active high, aligning with the typical SR latch operation description.
- Set Condition: To set Q to 1, S is taken high while R remains low.
- Reset Condition: To reset Q to 0, R is taken high while S remains low.
NAND Type SR Latch
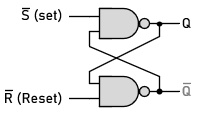
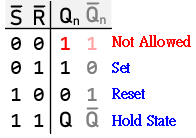
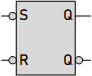
NAND-based SR Latch
- Structure: Consists of two cross-coupled NAND gates.
- Inputs Active Low: Both S and R inputs are active low due to the nature of NAND logic. This means that the normal state of S and R is high (1), and to activate an input, it must be brought low (0).
- Set Condition: To set Q to 1, S is taken low while R remains high.
- Reset Condition: To reset Q to 0, R is taken low while S remains high.
Gated SR Latch — SR Latch with Control Input
A standard SR latch is a fundamental building block in digital logic design. It offers two inputs (Set and Reset) and can hold a binary state (0 or 1). However, it lacks control over when the latch updates its state based on the inputs. This can be problematic in certain scenarios.
There are two common approaches to achieve a controlled SR latch:
- Gated SR Latch:
- This method uses additional logic gates (usually AND gates) before the original SR latch (made from NOR or NAND gates).
- An extra control signal, often called "Enable (EN)", is provided.
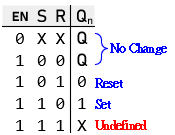
- When Enable is LOW, the AND gate outputs are forced LOW, regardless of the Set (S) and Reset (R) inputs. This effectively disables the latch, and the Q and Q outputs remain unchanged.
- When Enable is HIGH, the AND gates pass the S and R signals, allowing the SR latch to function normally based on these inputs.
- Clocked SR Latch (Edge-Triggered): (Will be discussed in next lesson)
- This approach introduces a clock signal along with the Enable input.
The latch updates its state only on a specific transition of the clock signal (e.g., positive or negative edge).
The S and R inputs are still used for setting and resetting, but their effect is only considered when the clock triggers the update.
- This approach introduces a clock signal along with the Enable input.
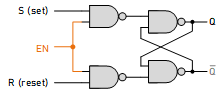
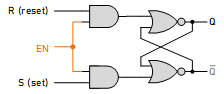
Advantages of SR Latch with Control
- Controlled SR latches offer more predictable behavior compared to a basic SR latch.
- The Enable or Clock input allows for synchronization with other circuits in a digital system.
- Gated SR latches provide simple control, while clocked SR latches become Synchronous SR Flip-Flops, offering precise edge-triggered updates.
Applications and Limitations
- The SR latch is used in digital circuits for simple storage tasks, such as storing a single bit of state information.
- It is a building block for more complex memory devices like flip-flops, counters, and registers.
- The major limitation is the forbidden state (both inputs high for NOR-based, or both low for NAND-based), which must be managed carefully in digital designs.
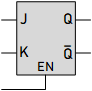
JK Latch
The JK latch is a type of sequential logic circuit, one of the fundamental building blocks in digital electronics. It's a bistable multivibrator, meaning it has two stable states that it can maintain indefinitely until triggered to switch. The JK latch expands on the functionality of simpler latches like the SR latch by resolving the ambiguous output state when both inputs are high.
Components of a JK Latch:
A basic JK latch can be constructed using NAND gates or NOR gates.
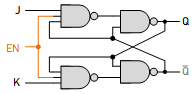
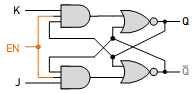

Circuit Description:
The JK latch consists of two cross-coupled NAND gates. Each output of a NAND gate is connected to one of the inputs of the other NAND gate. The J and K inputs are analogous to the S (set) and R (reset) inputs of an SR latch.
Inputs:
- J (Set Input): Setting this input high while the active EN sets the latch, driving the output Q to high.
- K (Reset Input): Setting this input high while the active EN resets the latch, driving the output Q to low.
- EN (optional in some configurations): Controls when the latch can change states. Changes to the output occur on the triggering level of the EN.
Behavior:
The JK latch operates with the following input conditions:
- J = 0, K = 0: No change. The latch retains its previous state.
- J = 0, K = 1: Reset. The output Q is set to low, and Q is set to high.
- J = 1, K = 0: Set. The output Q is set to high, and Q is set to low.
- J = 1, K = 1: Toggle. The output Q toggles to the opposite state (i.e., if Q is high, it becomes low, and vice versa).
D Latch
A D latch, also known as a Data latch or Transparent latch, is a fundamental sequential logic circuit that stores one bit of data (either 0 or 1) and holds it until it is updated.
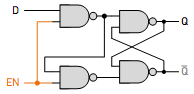
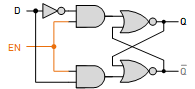
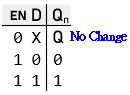
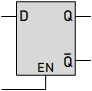
D Latch Operation:
- The Enable input (E) dictates the latch's transparency:
- When E is HIGH (active): The D Latch becomes transparent. The value at the Data input (D) is directly passed to the output (Q).
- When E is LOW (inactive): The D Latch becomes opaque. It holds its previous output (Q) regardless of the Data input (D).
T Latch
A T Latch, also known as a Toggle Latch, is a fundamental building block in digital circuits. It has a single data input (T) and an output (Q) that can hold a single bit (0 or 1). Unlike an SR Latch with separate Set and Reset inputs, a T Latch flips its output (toggles) on every positive or negative edge (depending on the design) of a clock signal.
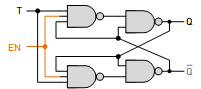
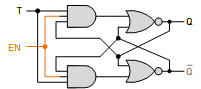
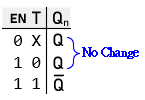
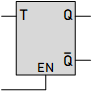
T Latch Operation:
- When the EN signal is LOW, the NAND gates act as buffers, and the current state of the latch (stored at Q) is maintained at the output.
- On an activated EN signal:
- If T is LOW (0), the output (Q) remains unchanged (holds the previous state).
- If T is HIGH (1), the output (Q) flips to its opposite state (toggles).
7.3 Flip-Flops
In a Digital Logic Circuits Design course, Flip-Flops (sometimes called Flip-Flops or simply FFs) are similar to latches but have a key difference: clock control. Flip-flops utilize a clock signal to determine when their outputs update based on the data inputs. Latches, on the other hand, can update their outputs immediately when the input conditions change.
Similarities to Latches:
- Flip-Flops share the same basic structure and functionalities as their latch counterparts (SR, JK, D, and T). They can store a single bit of data (0 or 1) and have mechanisms for setting, resetting, toggling, or storing data based on their type.
- You will find applications for Flip-Flops similar to those of latches, such as data synchronization, temporary storage, and state machines.
Key Difference - Clock Control:
- The defining characteristic of Flip-Flops is the presence of a clock input. This clock signal dictates when the Flip-Flop updates its output based on the data inputs.
- Latches update their outputs immediately when the input conditions change. Flip-Flops, however, only update their outputs on a specific transition of the clock signal (e.g., positive or negative edge). This introduces synchronization with other clocked elements in a digital circuit.
Types of Flip-Flops:
Just like latches, there are various Flip-Flops based on their functionalities and control mechanisms:
- SR Flip-Flop: Similar to an SR Latch but with a clock input. The Set, Reset, and clock determine the output update.
- JK Flip-Flop: Based on the JK Latch, it offers defined behavior for all input combinations, including a toggle operation on the clock edge.
- D Flip-Flop: Essentially a clocked version of a D Latch. The data input is captured at the output on the clock edge.
- T Flip-Flop: Similar to a T Latch, it uses a data input (T) and a clock signal. The output toggles on the clock edge if T is HIGH.
Advantages of Flip-Flops:
- Synchronization: The clock input allows precise control over when the Flip-Flop updates, ensuring proper timing within a digital system.
- Predictable Behavior: The clock-controlled updates eliminate the potential for race conditions that can occur in latches due to asynchronous input changes.
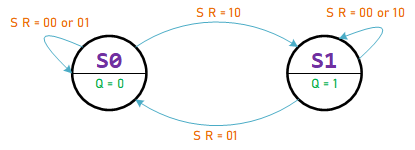
SR Flip-Flop
SR Flip-Flop - NOR Type
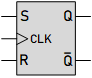
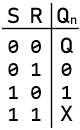

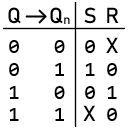
Characteristic Equation:
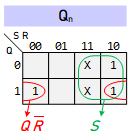
Characteristic Equation: ${Q_n} = S + Q\,\overline R \quad and\quad S\,R = 0$
SR Flip-Flop - NAND Type



Characteristic Equation:
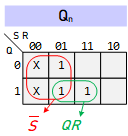
Characteristic Equation: ${Q_n} = \overline S + Q\,R\quad and\quad S + R = 1$
JK Flip-Flop


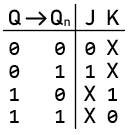
Characteristic Equation:
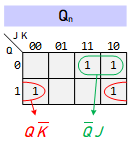
Characteristic Equation: ${Q_n} = Q\;\overline K + \overline Q \;J$
D Flip-Flop
A D Flip-Flop, also known as Data Flip-Flop or Delay Flip-Flop, is a fundamental building block in digital logic circuits commonly storing binary data. It is essentially a memory cell capable of storing one bit of information. A D flip-flop's basic operation is to capture the data input (D) value at a particular part of the clock cycle and then hold this value stable at the output (Q) until the next clock event.
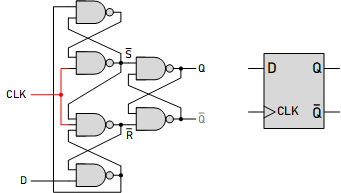
(a)
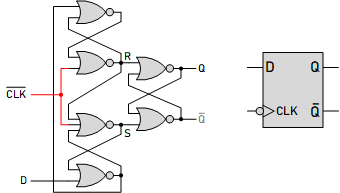
(b)
Figure: The Logic Circuits and Symbols for D Flip-Flop Triggered by the Clock Signal: (a) Rising Edge (b) Falling Edge
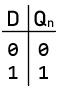


Characteristic Equation:
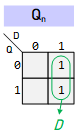
Characteristic Equation: ${Q_n} = D$
T Flip-Flop (Toggle Flip-Flop)
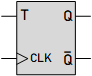
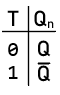
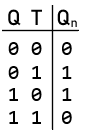
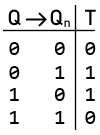
Characteristic Equation:
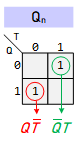
Characteristic Equation: ${Q_n} = Q \odot T$
The flip-flops can be described fully and uniquely by their logic symbol, characteristic table, characteristic equation, state diagram, or excitation table, and are summarized in the following Table.
| Name / Symbol | Characteristic Table | State Diagram / Characteristic Equations | Excitation Table |
|---|---|---|---|
SR |
 |
 ${Q_n} = S + Q\,\overline R \quad and\quad S\,R = 0$ |
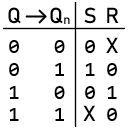 |
JK |
 |
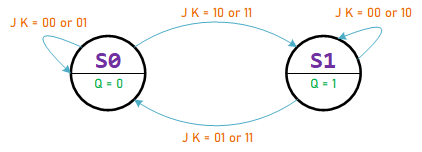 ${Q_n} = Q\;\overline K + \overline Q \;J$ |
 |
D |
 |
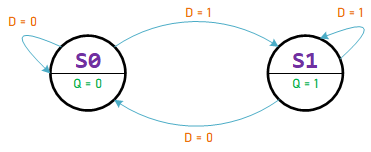 ${Q_n} = D$ |
 |
T |
 |
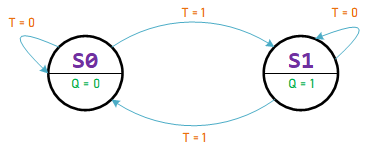 ${Q_n} = Q \odot T$ |
 |
7.4 Flip-Flop Conversion
Follow these steps for converting one flip-flop to the other.
- Begin by drafting the characteristic table for the flip-flop you intend to achieve.
- Write the excitation table for the sub-flip-flop that will be used.
- Complete the conversion table by inputting the necessary flip-flop inputs and derive the excitation table for the sub-flip-flop inputs.
- Create a Karnaugh Map (K-Map) to simplify the equation from the conversion table.
SR Flip-Flop to other Flip-Flop Conversions
SR Flip-Flop to other Flip-Flop Conversions
SR Flip Flop to JK Flip Flop
SR Flip Flop to JK Flip Flop

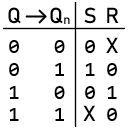
SR Flip Flop to D Flip Flop
SR Flip Flop to D Flip Flop

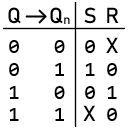
SR Flip Flop to T Flip Flop
SR Flip Flop to T Flip Flop

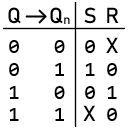
JK Flip-Flop to other Flip-Flop Conversions
JK Flip-Flop to other Flip-Flop Conversions
JK Flip-Flop to SR Flip-Flop
JK Flip-Flop to SR Flip-Flop


JK Flip Flop to D Flip Flop
JK Flip Flop to D Flip Flop


JK Flip Flop to T Flip Flop
JK Flip Flop to T Flip Flop


D Flip-Flop to other Flip-Flop Conversions
D Flip-Flop to other Flip-Flop Conversions
D Flip Flop to JK Flip Flop
D Flip Flop to JK Flip Flop


D Flip Flop to SR Flip Flop
D Flip Flop to SR Flip Flop


D Flip Flop to T Flip Flop
D Flip Flop to T Flip Flop


T Flip-Flop to other Flip-Flop Conversions
T Flip-Flop to other Flip-Flop Conversions
T Flip Flop to JK Flip Flop
T Flip Flop to JK Flip Flop


T Flip Flop to SR Flip Flop
T Flip Flop to SR Flip Flop


T Flip Flop to D Flip Flop
T Flip Flop to D Flip Flop


7.5 Applications
Case 01: Switch Debouncing
Switch Debouncing
Debouncing a push-button switch using an SR latch can effectively eliminate the issues caused by contact bounces during the switch's closing or opening. As depicted in the schematic, where VCC is the supply voltage and Rp is the pull-up resistor:
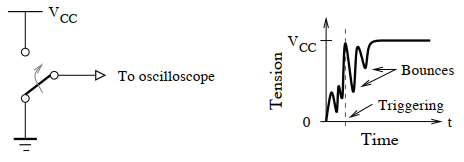
Figure: Waveform Illustrating Switch Contact Bounces
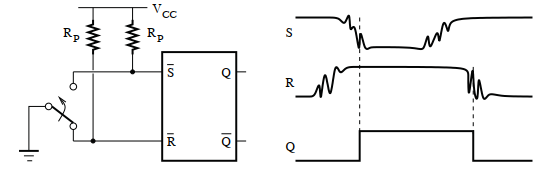

Figure: Debouncing Switch using a SR Latch
Configuration: The SR latch is connected so VCC provides the necessary supply voltage, and Rp serves as a polarization resistor, ensuring the latch inputs are correctly biased.
Operation with the Set Input (S):
- When the input S becomes logic level 1, the output Q of the latch is set to 1. This transition to high occurs at the first instance S reaches this state.
- After Q is set to 1, any further fluctuations or noise present at the S input will not affect the state of Q. Thus, the latch "ignores" any additional bounces or disturbances at the S input once it is set.
Operation with the Reset Input (R):
- Conversely, when the input S is at logic level 0, and R transitions to logic level 1 for the first time, the output Q of the latch is reset to 0.
- Like the set operation, once Q is reset to 0, further fluctuations at the R input do not alter the state of Q, ensuring stability and avoiding erroneous toggles due to switch bounce.
This setup utilizing an SR latch provides a stable and reliable state for the switch output, free from the transient fluctuations typically seen during mechanical switching operations. This ensures clean and consistent logic levels are delivered from the output Q of the SR latch, corresponding accurately to the physical state of the switch without the noise and errors introduced by bouncing.
Terminologies
Truth Table
- A truth table provides a complete listing of all possible input combinations and their corresponding output values for a combinational logic circuit.
- It covers all possible input states and shows the resulting output based on the logic function implemented by the circuit.
- Truth tables are commonly used for analyzing and designing combinational circuits, such as logic gates.
- Shows the relationship between inputs and outputs for all possible input combinations.
- It's the most fundamental table, like a dictionary lookup for a circuit's output based on the inputs.
Function Table
- A function table is essentially the same as a truth table.
- Applies to combinational circuits only.
- It can be used interchangeably with a truth table in many cases.
- May use different terminology for inputs and outputs (e.g., Input1, Output) compared to a truth table (A, B, F).
Characteristic Table
- A characteristic table (also known as a state table) describes the behavior of sequential circuits (e.g., flip-flops, registers).
- Shows the relationship between the circuit's current state, inputs, and next state.
- It may additionally include the output produced in the current state.
- It describes how the circuit's memory (state) changes based on inputs and how it affects the next output.
Excitation Table
- The excitation table is derived from the characteristic table.
- Applies to sequential circuits only (circuits with memory).
- Shows the input values required to transition the circuit from its current state to the next state.
- It helps design the control logic for flip-flops (circuits that store state) to achieve the desired behavior.
State Diagram
- Graphical representation of state table: these diagrams show states as nodes and transitions as directed arcs. They help visualize the behavior of the circuit over time.
State Table
- These tables list all possible states of the circuit and show the transitions between these states based on input values.
- Also called the transition table.
Here's a table summarizing the key differences:
| Feature | Truth Table / Function Table | Excitation Table | Characteristic Table | State Diagram | State table |
|---|---|---|---|---|---|
| Circuit Type | Combinational & Sequential (Truth Table) | Sequential Only | Sequential Only | Sequential Only | Sequential Only |
| Focus | Inputs & Outputs | Inputs for Next State | Current State, Inputs, Next State (and possibly Output) | Visual representation of state transitions | Tabular representation of state transitions |
| Information Provided | Output for each input combination | Inputs to cause a state transition | State transitions and possibly output | Graphical flow of states based on inputs | Tabular listing of next state and output for each state-input combination |
Analogy:
- Think of a truth table/function table as a simple instruction manual - if you give it these inputs, you get this output.
- An excitation table is like a recipe for changing state in a sequential circuit - use these inputs with the current state to get the desired next state.
- A characteristic table is like a detailed record of how a sequential circuit behaves - it shows how the state changes based on inputs and what the output is at each step.